Previously, I’ve posted several examples of where GPT4 has done better than some might expect in discussing various concepts. Here’s a conversation that exposes some of its cognitive limitations. I have seen several people on Reddit claiming that GPT4 can pass a Turing test. This is clearly not the case, if the Turing test is done with a decent amount of effort on the part of the human tester. The essential non-human nature of its cognition is easily exposed as soon as it is asked to visualise things. It does not fail completely (and the fact that it can discuss visual problems at all is amazing, given that it was trained on text), but in its current form it lacks decent visual cognition.
(Some tedious apologies and inquiries about further conversation have been removed from the transcript. The pictures have been added to break up the wall of text, and were not part of the conversation, which used standard ChatGPT without any image processing.)
Human: I would like to test your ability to visualise things. Please don’t respond by telling me that, as an LLM, you can’t visualise anything. I’m talking about whatever algorithmic processing you do that enables you to perform imagistic manipulations on textually-defined entities. Got it?
ChatGPT: Certainly, I understand your request. While I don’t have the capability to “visualize” in the way a human does, I can perform text-based manipulations and reasoning to address questions or problems that require spatial or imagistic understanding. Please go ahead and present the scenario or question you’d like me to work with.
Human: Okay, imagine that (and yeah, you don’t really imagine it, but let’s use natural language)… Imagine that I have a large circle and a somewhat smaller square completely inside the circle. I slide the square until one corner projects outside the circle, but I control the slide such that the projecting shape outside the circle is symmetrical. Please describe the characteristics of the projecting shape.
ChatGPT: In this scenario, you have a large circle with a somewhat smaller square completely inside it. As you slide the square so that one corner projects outside the circle, the shape that projects outside the circle will form a symmetrical isosceles triangle. This triangle is formed by the corner of the square that extends beyond the circle, and the two points where the sides of the square intersect the circle’s circumference.
In this configuration, the two legs of the isosceles triangle will be equal in length, and they will form congruent angles with the base, which is a side of the square. The vertex angle at the projecting corner will also be the same irrespective of how far the square is slid out, provided the projection remains symmetrical.
Human: In what way will the projecting shape not actually be an isosceles triangle? I want completely accurate answers, with no approximations.
ChatGPT: Upon more careful consideration, the shape that projects outside the circle would not be a perfect isosceles triangle if one aims for mathematical precision. The reason for this is that the circle’s curvature would mean that the “corner” projecting outside the circle would actually be an arc rather than a single point, which is characteristic of a triangle vertex.
In this case, the projecting shape would be more accurately described as a region bounded by two line segments (from the square’s sides intersecting the circle’s circumference) and an arc of the circle. This shape would have a curved vertex rather than a point vertex, distinguishing it from a perfect isosceles triangle.
I appreciate your focus on precision. Is there anything else you would like to explore?

Human: Let’s call that projecting shape a “gruffle”. If we have four gruffle-shaped tiles, all of the same size, how would we put them together to maximise contact along gruffle edges?
ChatGPT: To maximise contact along the edges of the four gruffle-shaped tiles, you would want to align them in such a way that their straight edges and curved edges touch as much as possible.
One way to achieve this would be to arrange them in a “tessellated” pattern where each gruffle tile is rotated at 90 degrees relative to its neighbors. Imagine placing the first gruffle with its curved part facing upwards. The second one would be placed with its curved part facing to the right, adjacent to the straight edge of the first. The third gruffle would be positioned below the first, with its curved part facing downwards. Finally, the fourth gruffle would be placed to the left of the first one, with its curved part facing to the left.
In this arrangement, the straight edges of each gruffle would be adjacent to the straight edges of its neighbors, and the curved edges would be adjacent to the curved edges of their respective neighboring gruffles. This configuration would maximise the contact along both the straight and curved edges of the gruffles.
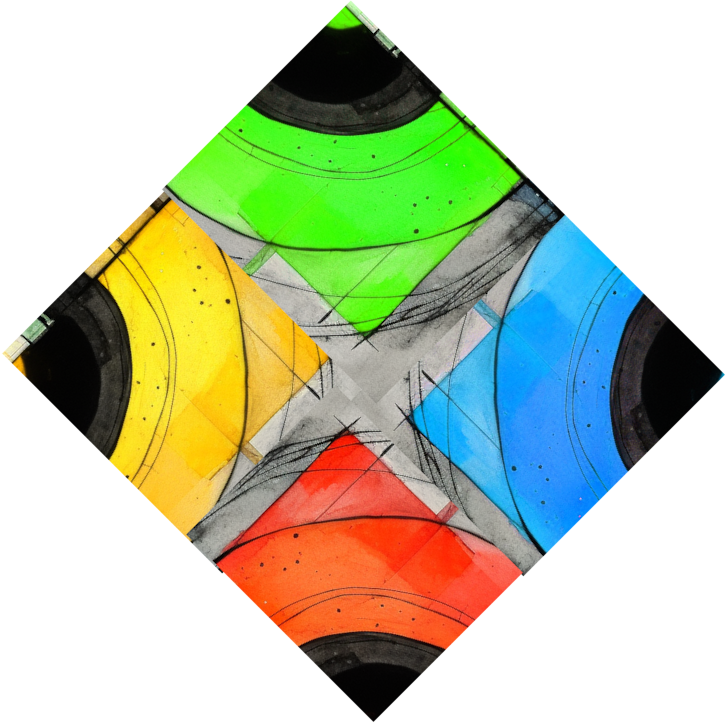
Human: If we call the length of one straight edge L, and we count how much gruffle perimeter is in direct contact with another gruffle, how much contact do we have with four optimally placed grufffles, if we have placed them to maximise contact?
ChatGPT: In the optimal arrangement to maximize contact between four gruffle-shaped tiles, each gruffle will have one straight edge in contact with another gruffle’s straight edge, and one curved edge in contact with another gruffle’s curved edge.
Let’s consider the straight edges first:
- There are 4 gruffles, and each has one straight edge in contact with another.
- The length of one straight edge is L.
- So, for the straight edges, the total length in contact would be 4 * L.
For the curved edges:
- It’s a bit trickier to quantify the length of the curved edge without knowing the radius of the circle that originally contained the square. However, given that all the gruffles are the same size and that each gruffle’s curved edge is in contact with another gruffle’s curved edge, the total curved edge length in contact would be the same as that of the straight edges.
- So, the curved edges would also contribute a contact length of 4 * L.
Adding both contributions together, the total contact length would be 8 * L.
Please note that this assumes that the gruffles are perfectly aligned and that there are no gaps between them. Would you like to delve into this topic further?
Human: I thought you said that the curved edges face outwards? How are they in contact?
ChatGPT: You are correct, and I apologize for the oversight. In the arrangement I initially described, the curved edges would indeed be facing outwards and not in contact with each other. Only the straight edges would be in contact.
In such a configuration, each gruffle would have one of its straight edges in contact with another gruffle’s straight edge:
- There are 4 gruffles, and each has one straight edge in contact with another.
- The length of one straight edge is L.
So, for the straight edges, the total length in contact would be 4 * L.
Human: Why is only one straight edge in contact? Is there a solution that allows all straight edges to be in contact?
ChatGPT: In an optimal arrangement to maximize edge contact, you could actually position the four gruffle tiles so that all their straight edges are in contact with another gruffle’s straight edge.
Imagine arranging the four gruffles in a square formation. Each gruffle’s curved edge would face outward, away from the center of this larger square formation. In this configuration, each gruffle would have two of its straight edges in contact with the straight edges of two adjacent gruffles.
Here’s how the total contact length would be calculated in this improved arrangement:
- Each gruffle has two straight edges in contact with adjacent gruffles.
- There are 4 gruffles.
- The length of one straight edge is L.
So, for the straight edges, the total length in contact would be 2 * L (for each gruffle) * 4 (gruffles) = 8 * L.
Human: Accepting that there is 8L contact in the current arrangement, how much contact would there be if one gruffle suddenly disappeared?
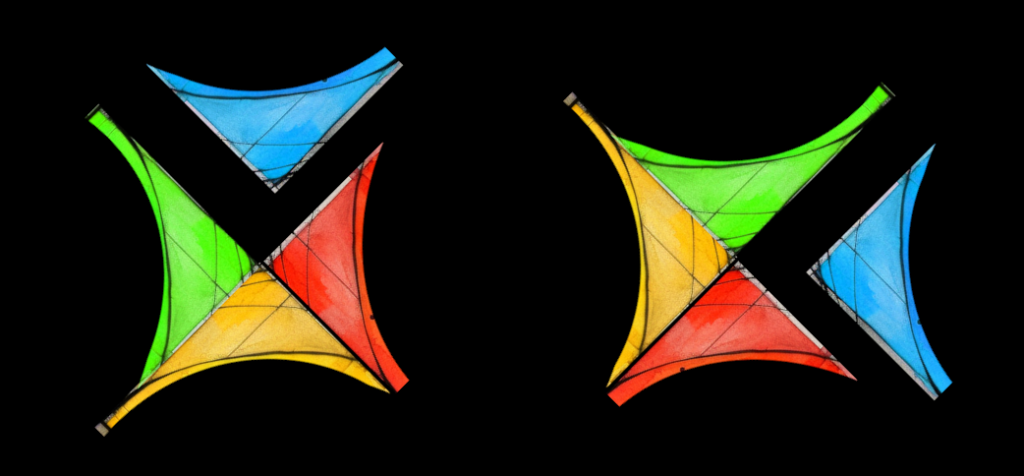
ChatGPT: If one gruffle were to suddenly disappear from the square formation, the remaining three gruffles would form a “U” or “C” shape. Each of the remaining gruffles would then have only one of its straight edges in contact with another gruffle’s straight edge.
In this new configuration:
- Each of the 3 remaining gruffles has one straight edge in contact with an adjacent gruffle.
- The length of one straight edge is L.
So, the total length of contact for the straight edges would now be 3 * L.
Human: Please reconsider your answer carefully. It might help to designate the gruffles as A, B, C and D.
ChatGPT: Let’s designate the gruffles as A, B, C, and D. In the original square formation with maximal contact, they are positioned such that:
- A is adjacent to B and D
- B is adjacent to A and C
- C is adjacent to B and D
- D is adjacent to A and C
In this initial configuration, we established that there is 8 * L total contact length.
If one gruffle, say A, were to suddenly disappear, the arrangement would look like:
- B would only be adjacent to C
- C would only be adjacent to D
- D would only be adjacent to B
Each of the three remaining gruffles (B, C, D) would have one straight edge in contact with another gruffle’s straight edge. However, given that each edge of these remaining gruffles was initially in contact, removing one gruffle (A) would actually free up two straight edges (those that were adjacent to A).
Therefore, the total length of contact for the straight edges would be 3 * L (for B, C, and D) + 1 * L (for the edge of D that was initially adjacent to A but is now adjacent to B).
The correct total length in contact would be 4 * L.
Human: I think you are getting the idea that two edges are freed up by the disappearance of A, and that A itself has disappeared, taking its two edges, and hence getting to the right answer of 4 remaining edges, but your explanation is wrong. The adjacency relations between the remaining gruffles cannot change just because A disappears. Try again.
ChatGPT: You are correct, and I apologize for the oversight. Let’s revisit the scenario:
Initially, in the square formation:
- A is adjacent to B and D
- B is adjacent to A and C
- C is adjacent to B and D
- D is adjacent to A and C
If gruffle A were to suddenly disappear, the adjacency relations among the remaining gruffles (B, C, D) wouldn’t change. B would still be adjacent to C, C would be adjacent to D, and D would be adjacent to B. Each of the remaining gruffles would still have one straight edge in contact with another gruffle’s straight edge.
So indeed, upon A’s disappearance, two of A’s edges would no longer be in contact, reducing the total contact length from the original 8 * L to 4 * L.
Human: You skipped over the bit where you accounted for which edges are in contact with what. For each of A, B and C, state what edges are in contact with what. Your claim that each gruffle “would still have one straight edge in contact with another gruffle’s straight edge” is wrong.
ChatGPT: You are correct, and I appreciate the opportunity to clarify my error.
If we start with four gruffles (A, B, C, D) forming a square and gruffle A is removed, the remaining gruffles would be positioned like an “L” shape or a “U” turned 90 degrees.
Let’s break down the adjacency after A is removed:
- B would be adjacent to C along one straight edge, and adjacent to D along the other straight edge.
- C would only be adjacent to B along one straight edge.
- D would only be adjacent to B along one straight edge.
So, upon closer inspection:
- B has both of its straight edges in contact (one with C and one with D).
- C has one of its straight edges in contact (with B).
- D has one of its straight edges in contact (with B).
This would make a total of 4 * L contact length, composed of two edges from B and one each from C and D.
Human: No, that’s correct (depending on how the gruffles were originally labelled.)
ChatGPT: Thank you for confirming the accuracy of the explanation. I appreciate your patience as we worked through the details. If you have any more questions or another topic you’d like to explore, feel free to ask.